All Possible Row Canonical Matrices with Binary Entries

The other day I ran across a linear algebra problem which asked the reader to enumerate all possible 2x2 and 3x3 row canonical matrices (RCMs, aka row echelon form matrices) with binary entries {0, 1}. For those unfamiliar, a row canonical matrix is a matrix with the following properties:

• All zero rows, if any, are at the bottom of the matrix.
• Each leading nonzero entry in a row is to the right of the leading nonzero entry in the preceding row.
• Each pivot (leading nonzero entry) is equal to 1 (we get this by default for our problem).
• Each pivot is the only nonzero entry in its column.

As it turns out there are five 2x2 and sixteen 3x3 matrices of this form:
This problem gave me the hankering to develop a formula to determine the number of RCMs with binary entries for a square matrix of order N. The first order of business in this endeavour was to develop a program to count the number of RCMs with binary entries of order N to see if there was an obvious pattern and spot-check the formula once completed.

public class RowCanonicalForm {
	public static void main(String...args) {
		for(int n = 1; n < 10; System.out.println(n + "x" + n + ": " + populate(new boolean[n][n++], 0, 0)));
	}
	
	private static int populate(boolean[][] matrix, int i, int j) {
		if (!isRowCanonicalForm(matrix)) return 0;
		if (j == matrix.length) {i++; j = 0;}
		if (i == matrix.length) return 1;
		return populate(matrix, true, i, j) + populate(matrix, false, i, j);
	}
	
	private static int populate(boolean[][] matrix, boolean value, int i, int j) {
		matrix[i][j] = value;
		return populate(matrix, i, j+1);
	}

	private static boolean isRowCanonicalForm(boolean[][] matrix) {
		int minZeroRow = Integer.MAX_VALUE, maxNonZeroRow = 0;
		Integer pivot = null, lastPivot = null;
		for(int i = 0; i < matrix.length; i++) {
			pivot = null;
			for(int j = 0; j < matrix.length; j++) {
				if (matrix[i][j]) {
					if (i >= 1 && (((lastPivot==null)?Integer.MAX_VALUE-1:lastPivot) >= j)) return false;
					for(int i2 = 0; i2 < matrix.length; i2++) if ((i2 != i) && matrix[i2][j]) return false;
					pivot = j;
					maxNonZeroRow = i;
					break;
				}
			}
			minZeroRow = (pivot == null)?Math.min(minZeroRow, i):minZeroRow;
			if (maxNonZeroRow > minZeroRow) return false;
			lastPivot = pivot;
		}
		return true;
	}	
}

This program produces the following results:

nxn	f(n)
1x1	2
2x2	5
3x3	16
4x4	67
5x5	374
6x6	2,825
7x7	29,212
8x8	417,199
9x9	8,283,458

After a bit of research and some fiddling around it became clear that f(n) was equivalent to the summation of Gaussian binomial coeffecients with a q-number of 2. So, what does the final formula look like?




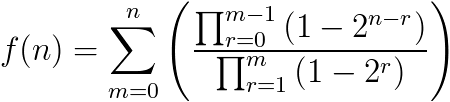
As you can see, even the formula requires a bit of work to determine the number of RCMs with binary entries! The below program implements the formula in an attempt to make calculation simpler. Feel free to verify that the results from this program matches that of the above.

import java.math.BigInteger;
import java.text.DecimalFormat;
import java.text.NumberFormat;

public class RowCanonicalFormCount {
	public static void main(String...args) {
		NumberFormat format = DecimalFormat.getNumberInstance();
		for(int i = 1; i <= 50; System.out.println(i + "\t" + format.format(f(i++))));
	}
	
	private static BigInteger f(int n) {
		BigInteger sum = BigInteger.ZERO;
		for(int m = 0; m <= n; m++) {
			BigInteger num = BigInteger.ONE, den = BigInteger.ONE;
			for(int r = 0; r <= (m - 1); r++) {
				num = num.multiply(BigInteger.ONE.subtract(BigInteger.valueOf(2).pow(n-r)));
			}
			for(int r = 1; r <= m; r++) {
				den = den.multiply(BigInteger.ONE.subtract(BigInteger.valueOf(2).pow(r)));
			}
			sum = sum.add(num.divide(den));
		}
		return sum;
	}	
}

Non-Binary Entries

What about RCMs with non-binary entries? The table below contains the valid RCM permutation counts for the number of allowed digits (q=2 means {0, 1}, q=3 means {0, 1, 2}, ...). These values are generated by the code below the table, a modified version of the code at the top of this page, which for each "free" entry (doesn't have to be zero or one for the matrix to remain an RCM matrix) accounts for all possible values.

nxn	q=2	q=3	q=4	q=5	q=6
1x1	2	2	2	2	2
2x2	5	6	7	8	9
3x3	16	28	44	64	88
4x4	67	212	529	1,120	2,111
5x5	374	2,664	12,278	42,176	118,182
6x6	2,825	56,632	565,723	3,583,232	16,649,389
7x7	29,212	2,052,656	5,1409,856	666,124,288	5,547,079,988
8x8	417,199	127,902,864	9,371,059,621	281,268,665,344	4,671,840,869,691

public class RowCanonicalFormNonBinary {
	// The number of int values allowed (including 0 and 1)
	// 2 = binary entries {0, 1}
	// 3 = entries of possible values {0,1,2} (so long as the leading non-zero entry in a row is 1)
	// 4 = {0,1,2,3}
	// ...
	private static final long Q = 4;
	
	public static void main(String...args) {
		for(int n = 1; n < 10; System.out.println(n + "x" + n + ": " + populate(new boolean[n][n++], 0, 0)));
	}
	
	private static long populate(boolean[][] matrix, int i, int j) {
		if (!isRowCanonicalForm(matrix)) return 0;
		if (j == matrix.length) {i++; j = 0;}
		if (i == matrix.length) return pow(Q-1, getVariableEntriesCount(matrix));
		return populate(matrix, true, i, j) + populate(matrix, false, i, j);
	}
	
	private static long populate(boolean[][] matrix, boolean value, int i, int j) {
		matrix[i][j] = value;
		return populate(matrix, i, j+1);
	}

	private static boolean isRowCanonicalForm(boolean[][] matrix) {
		long minZeroRow = Integer.MAX_VALUE, maxNonZeroRow = 0;
		Integer pivot = null, lastPivot = null;
		for(int i = 0; i < matrix.length; i++) {
			pivot = null;
			for(int j = 0; j < matrix.length; j++) {
				if (matrix[i][j]) {
					if (i >= 1 && (((lastPivot==null)?Integer.MAX_VALUE-1:lastPivot) >= j)) return false;
					for(int i2 = 0; i2 < matrix.length; i2++) if ((i2 != i) && matrix[i2][j]) return false;
					pivot = j;
					maxNonZeroRow = i;
					break;
				}
			}
			minZeroRow = (pivot == null)?Math.min(minZeroRow, i):minZeroRow;
			if (maxNonZeroRow > minZeroRow) return false;
			lastPivot = pivot;
		}
		return true;
	}
	
	private static long pow(long b, long p) {
		long r = 1;
		for(long i = 1; i <= p; i++) {
			r *= b;
		}
		return r;
	}
	
	private static long getVariableEntriesCount(boolean[][] matrix) {
		long count = 0;
		for(int i = 0; i < matrix.length; i++) {
			boolean found = false;
			for(int j = 0; j < matrix.length; j++) {
				if (matrix[i][j]) {
					if (found) count++;
					found = true;
				}
			}
		}
		return count;
	}
}

Unsurprisingly, the values are equivalent to the summation of Gaussian binomial coeffecients with the specified q-number, with the same formulation as the original formula, with the "2" replaced by the q-number you are working with. You can verify this by replacing the line "BigInteger.valueOf(2)" in the second code sample with "BigInteger.valueOf(q)", where q represents the q-number.